Nezávislosť dvoch premenných na sebe môžeme merať pomocou Chí kvadrát štatistiky.
Chí kvadrát (Chi-Square – χ2)
Chí-kvadrát test sa používa na porovnanie distribúcie kategorickej premennej v skupine (pozostávajúcej z kategórií, napr. druh vzdelania, rodinný stav, fajčiar/nefajčiar, atď.) s distribúciou v inej skupine. Ak sa distribúcia kategorickej premennej v rôznych skupinách príliš nelíši, môžeme konštatovať, že distribúcia kategorickej premennej nesúvisí so skupinami. Alebo môžeme povedať, že kategorická premenná a skupiny sú nezávislé. Napríklad, ak je medzi mužmi viac fajčiarov ako medzi ženami, je väčšia šanca nájsť fajčiara medzi mužmi ako medzi ženami. V tomto prípade môžeme konštatovať, že pohlavie nie je nezávislé od toho, či ide o fajčiara alebo nie (čiže existuje tu závislosť). Ak existuje rovnaká šanca, či niekto fajčí alebo nie medzi mužmi a ženami, zistíme, že šanca na pozorovanie stavu je rovnaká bez ohľadu na pohlavie a môžeme uzavrieť ich vzťah ako nezávislý.
Chí kvadrát je založený na porovnávaní pozorovaných (nameraných) – empirických početností (observed count) s očakávanými početnosťami (expected count). Očakávaná početnosť by platila pre bunku vtedy, ak by platila nulová hypotéza o nezávislosti, teda ak by boli premenné úplne nezávislé.
Tento test sa používa ako test nezávislosti pri overovaní hypotéz:
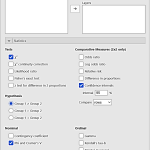
Test chí kvadrát by sa nemal používať, ak viac ako 20% polí má očakávanú početnosť menšiu ako 5 a minimálna očakávaná početnosť nesmie byť menšia ako 1 (Rabušic, Soukup, Mareš, 2019, str. 261). V prípade, že nie je dodržaná podmienka o očakávanej početnosti menšej ako 5, sa odporúča použiť Fisherov exaktný test (Fisher’s exact test).
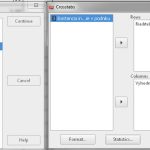
PRÍKLAD – TEST NEZÁVISLOSTI (Chi-Square Test of Independence):
Zadanie:
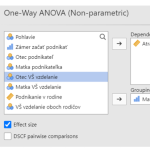
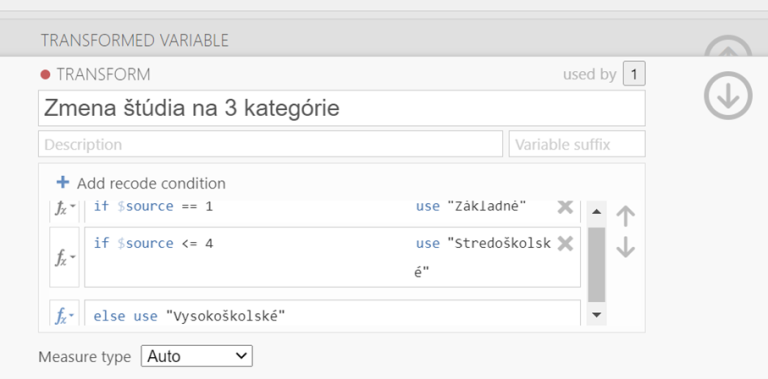
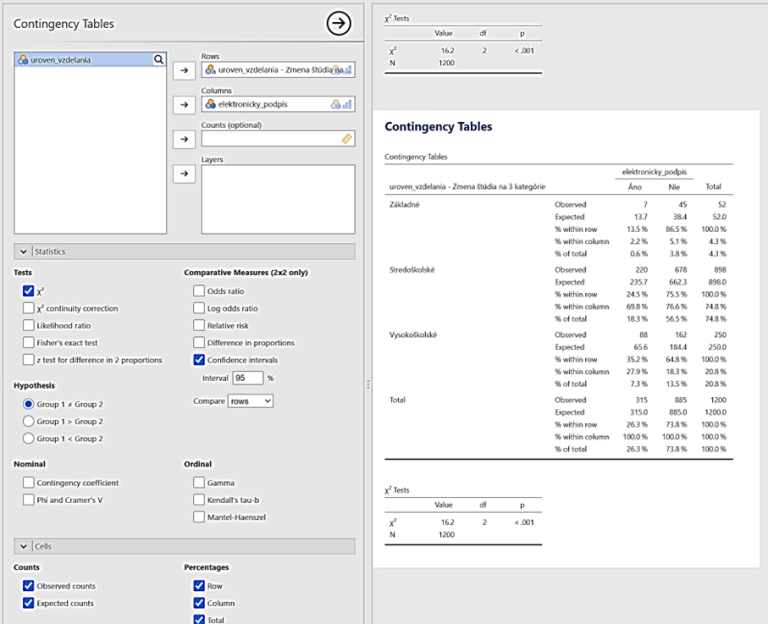
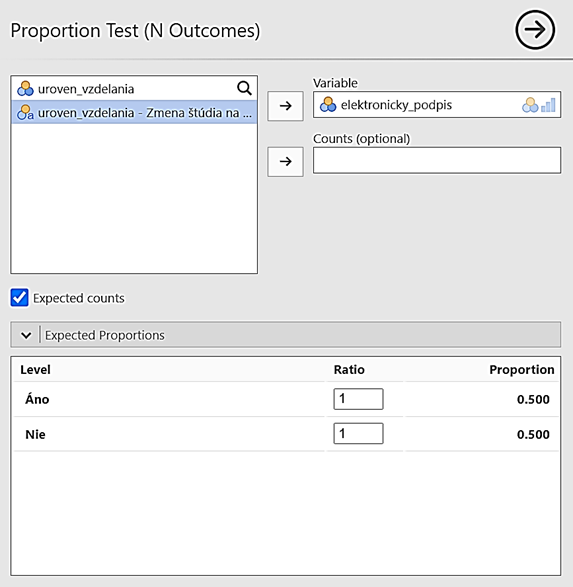
Zistite, či existuje vzájomná súvislosť medzi úrovňou vzdelania a aktivovaním si elektronického podpisu v občianskom preukaze.
Riešenie:
Pre skúmanie týchto dvoch premenných si stanovíme hypotézu na základe predpokladu, že ľudia s vyšším vzdelaním budú mať väčšiu tendenciu k používaniu informačných technológií ako ľudia s nižším vzdelaním. Budeme predpokladať, že existuje vzťah medzi úrovňou vzdelania a počtom aktivovaných elektronických certifikátov v občianskych preukazoch.
H1: Úroveň vzdelania súvisí s tým, či je alebo nie je aktivovaný elektronický certifikát v občianskom preukaze.
H0: Úroveň vzdelania nesúvisí s tým, či je alebo nie je aktivovaný elektronický certifikát v občianskom preukaze.
Príklad spracujte v nasledovnom súbore
Niektoré dátové súbory program Jamovi nevie otvoriť priamo kliknutím na súbor.
Takéto súbory potom otvoríte nasledovne:
Pre výpočet použijeme súbor elektronicky_certifikat+uroven_vzdelania.omv, ktorý obsahuje dve premenné:
Ešte pred tým, ako sme pristúpili k analýze, pre zlepšenie prehľadnosti sme zoskupili kategórie v rámci úrovne vzdelania zo siedmich do troch. Toto sme spravili v časti Variables, kde sme si označili premennú, ktorú chcem upravovať, v našom prípade uroven_vzdelania a cez voľbu Transform sme si vytvorili novú transformovanú premennú, ktorú sme si označili uroven_vzdelania – Zmena štúdia na 3 kategórie, kde sme si určili, že kategória s kódom 1 sa bude volať „Základné“, kategórie s číslami menšími alebo rovnými ako 4 sa budú nazývať „Stredoškolské“ a ostatné kategórie budú „Vysokoškolské“. Zdrojovou premennou pre túto premennú je uroven_vzdelania.
Následne sme pristúpili k výpočtu chí-kvadrát, ktorý zrealizujeme cez voľbu v hornom hlavnom menu programu Analýzy (Analyses) – Frekvencie (Frequencies) – Kontingenčné tabuľky (Contingency Tables – Independent Samples). Do riadkov (rows) presunieme premennú uroven_vzdelania – Zmena štúdia na 3 kategórie a do stĺpcov (columns) premennú elektronicky podpis (nie je podstatné, ktorá premenná ide do riadku a ktorá do stĺpcov). V časti Bunky (Cells) začiarkneme všetky možnosti.
Interpretácia:
Na základe štatistickej významnosti testu chí-kvadrát p < 0,001 (hladina významnosti je menšia ako hodnota 0,05) prijmeme hypotézu H1 a zamietneme hypotézu H0, čiže medzi úrovňou vzdelania a aktiváciou elektronického podpisu v občianskom preukaze existuje štatisticky významná súvislosť.
Alebo formulácia v angličtine:
It was found that people with a university education were significantly more likely to have activated electronic signature than those with lower education, X2 (N = 1200, 2) = 162, p < 0,001.
Pomôcka:
X2 (N = počet účastníkov, df) = chí-kvadrát, p = hodnota p.
PRÍKLAD – Test dobrej zhody (Chi Square Goodness of Fit):
Štatistiky chí-kvadrát je možné použiť aj v oblasti jednorozmernej analýzy pre testovanie hypotéz o rozložení hodnôt jednej premennej.
Zadanie:
Zistiť, či je rozloženie osôb, ktoré si aktivovali elektronický podpis a tých, ktoré si ho neaktivovali rovnomerne rovnaké alebo nie je.
Riešenie:
Pre tento účel opäť použijeme rovnaký dátový súbor ako v predchádzajúcom príklade a stanovíme sa tieto hypotézy:
H1: Rozloženie osôb, ktoré si aktivovali elektronický podpis v občianskom preukaze a tých, ktorý si ho neaktivovali, nie je rovnomerne rovnaké.
H0: Rozloženie osôb, ktoré si aktivovali elektronický podpis v občianskom preukaze a tých, ktorý si ho neaktivovali, je rovnomerne rovnaké.
Použijeme test z kategórie Frequencies – N Outcome (X2 Goodness of fit). Ako premennú (Variable) zadáme elektronický podpis. Nižšie začiarkneme aj voľbu očakávané hodnoty (Expected counts).
Výsledky testu sú zobrazené vo forme kontingenčnej tabuľky a výsledkov testu pod ňou. V kontingenčnej tabuľke vidíme v riadkoch pozorované (Observed), koľko z respondentov si vybralo danú voľbu. V riadkoch označených očakávané (Expected) môžeme vidieť, akú hodnotu početnosti by daná voľba mala mať, ak by boli odpovede rovnomerne rozložené cez všetky možnosti (v našom prípade N = 1200 / 2 = 600). Štatistická významnosť testu vyšla menšia ako 0,05, čiže výsledky v kontingenčnej tabuľke sú štatisticky významné.
Interpretácia:
Na základe štatistickej významnosti testu chí-kvadrát p < 0,001 (hladina významnosti je menšia ako hodnota 0,05) prijmeme hypotézu H1 a zamietneme hypotézu H0, čiže medzi tým, či si respondenti aktivovali alebo neaktivovali elektronický podpis v občianskom preukaze je štatistický významný rozdiel. Až 74% respondentov si elektronický podpis neaktivovalo.
Spracoval Matej Černý, Máj 2022
Táto webstránka je súčasťou projektu KEGA projekt č. 016EU-4/2021 s názvom: Inovácia študijného programu prostredníctvom vypracovania novej modernej vysokoškolskej učebnice s názvom: „Metodológia a metódy vedeckého výskumu v manažmente, s podpornými didaktickými prostriedkami.“. Tento grant udelilo Ministerstvo školstva, vedy, výskumu a športu slovenskej republiky.
© Copyright
