Zadanie:
Porovnajte celkové skóre v intuícii u mužov a u žien.
Riešenie:
Muži a ženy sú dve nezávislé skupiny v súbore, teda jedna druhú neovplyvňujú. Preto použijeme t – test pre dva nezávislé výbery (Independent samples T test). Mužov máme v súbore kódovaných v stĺpci pohlavie ako 1 a ženy ako 2. Pri porovnávaní skupín odporúčam stanoviť si hypotézy, ktoré nám pomôžu lepšie si ujasniť skúmanú otázku a vnímať problém exaktnejšie.
Stanovenie hypotéz:
H0 : Muži sa štatisticky významne neodlišujú od žien v sumárnom skóre škály PID intuícia.
H1 : Muži sa štatisticky významne odlišujú od žien v sumárnom skóre škály PID intuícia.
Z týchto dvoch hypotéz platí len jedna, pomocou štatistickej analýzy zistíme, ktorá to je.
Klikneme Analyzovať (Analyze) → Porovnanie priemerov (Compare means) → T – test pre dva nezávislé výbery (Independent samples T test)
V dialógovom okne potom musíme vybrať z ktorých premenných sa bude t – test (y) počítať, tie sú označené ako Test Variable (s). Môžeme vybrať jednu premennú alebo aj viac. Ak vyberieme viac premenných PSPP softvér vypočíta výsledky pre všetky premenné a zobrazí ich v sumárnej tabuľke. V dialógovom okne treba ešte vybrať skupiny, ktoré má softvér porovnávať. Tie sú označené ako premenné pre skupiny (Grouping Variable). V našom prípade je to pohlavie, ktoré je rozdelené na dve skupiny muži a ženy. Softvér od nás vyžaduje zadefinovať skupiny (Define Groups), ktoré označuje ako hodnota pre skupinu 1 – muži (Group1 value) a hodnota pre skupinu 2 – ženy (Group2 value). V našom prípade sem zadáme 1 a 2.
Výsledky:
Program PSPP vytvorí dve tabuľky
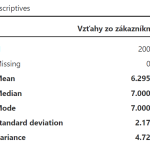
V prvej tabuľke sú opisné štatistiky. Priemerné skóre mužov (n = 137 – počet mužov) bolo 30,92, SD = 5,18 a pre ženy (n = 358) bol priemer 30,31 bodov a smerodajná odchýlka 5,07. Pri porovnávaní týchto čísel vidíme, že rozdiel je malý. Nás však zaujíma, či je rozdiel systematický a nielen spôsobený náhodou. To nám pomôže zodpovedať druhá tabuľka, ktorá dáva odpoveď na to, či je rozdiel medzi skupinami dostatočne veľký, aby bol štatisticky významný. To je oveľa viac ako 0,05, preto konštatujeme, že rozdiel medzi ženami a mužmi nie je štatisticky významný.
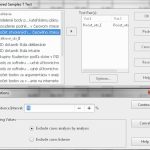
V druhej tabuľke sú uvedené výsledky Levenovho testu na rovnosť rozptylov. Tento test meria normalitu rozloženia dát. A hodnota Sigma (p hodnota) je menšia ako 0,05, potom musíme použiť iný typ testu (neparametrický test Mann – Whitney Test) V našom prípade je hodnota vyššia (p = 0,691) a tak môžeme použiť výsledky, ktoré nám vyšli v ďalších stĺpcoch.
Hypotézu H1 sme si stanovili tak, že rozdiel medzi skupinami bude existovať, teda predpokladáme rovnakú viarianciu (Equal variances assumed). Tá je uvedená v prvom riadku. Zaujíma nás hladina významnosti p pre obojstranne testovanú hypotézu – tu označená ako Sig. (2 – tailed). Tá v našom prípade bola p = 0,234.
Interpretácia (náš príklad):
Muži (M = 30,92 , SD = 5,18) sa štatisticky významne nelíšia od žien (M = 30,31 , SD = 5,07) v dosiahnutom skóre PID intuícia (t = 1,19, p = 0,234).
Medzinárodná – anglická interpretácia, príklady (nesúvisí s naším príkladom):
Prípad 1:
Then we used t-test for comparing intuitive and deliberative participants in the number of opened clues first in condition of time stress and then in no time stress condition. Results showed that there was difference in information search between conditions (t = – 8.043; p = .000) – participants engaged in more information search in condition of no time stress (12.35 vs. 15.6 opened clues). (Čavojová, Hanák, 2014)
Prípad 2:
The mean subjective probability perception was again higher in the “1 in 200” condition compared to the “5 in 1000” condition (respectively, M = 3.40, SD = 1.73; M 2.79, SD = 1.74). However, this difference was not statistically significant, t(94) = 1.71, p = .09, d = 0.35. (Sirota, et. al. 2014)
Spracoval Róbert Hanák, Október 2015
Táto webstránka je súčasťou projektu KEGA projekt č. 016EU-4/2021 s názvom: Inovácia študijného programu prostredníctvom vypracovania novej modernej vysokoškolskej učebnice s názvom: „Metodológia a metódy vedeckého výskumu v manažmente, s podpornými didaktickými prostriedkami.“. Tento grant udelilo Ministerstvo školstva, vedy, výskumu a športu slovenskej republiky.
© Copyright
